In a compartment fire, the upper layer presents a number of hazards to firefighters including the fact that 1) Smoke is fuel, and 2) the upper layer can be extremely hot. Application of an appropriate amount of water fog into the upper layer reduces the potential for ignition and lowers the temperature of the gases (reducing thermal load on the firefighters working below). While this sounds simple, and fairly intuitive, this basic technique to control upper layer hazards is frequently misunderstood. This is the first in a series of posts that will attempt to provide a simple explanation of the science behind gas cooling as a fire control technique.

How Does it Work

When a pulse (brief application) of water fog is applied into a layer of hot smoke and gases with a temperature of 500^o C (932^o F) what happens? As the small droplets of water pass through the hot gas layer, energy is transferred from the hot smoke and gases to the water. If done skillfully, the upper layer will not only be cooler and lest likely to ignite, but it will contract (or at least stay the same volume) providing a safer working environment below.

As demonstrated by Superintendent Rama Krisana Subramaniam, Bomba dan Penelamat (Fire & Rescue Malaysia) a short pulse can place a large number of small water droplets in the upper layer that develops during a compartment fire (see Figure 1).

Figure 1. Short Pulse

When presenting this concept, firefighters often present me with two questions:

• Since water expands approximately 1700 times when turned to steam at 100^o C, why doesn’t the upper layer drop down on top of the firefighters?
• How can such a small amount of water have such a dramatic effect on the fire environment?

Math or No Math?

Using a bit of math, there is a really good explanation as to how gas cooling really works. The best answer is a bit complex, but a good conceptual explanation can be accomplished with a minimal amount of math.

Heating the water to 100^o C (212^o F) and production of steam transfers a tremendous amount of energy from the hot smoke and gases to the water, reducing the temperature of the hot gases. As the temperature of the hot gases is reduced so is their volume. However, don’t forget about the steam.

When water is turned to steam, it expands. At its boiling point, water vaporized into steam will expand 1700 times. A single liter of water will produce 1700 liters (1.7 m³) of steam. The expansion ratio when water is vaporized is significant. However, due to the tremendous amount of energy required to vaporize the water (and resulting reduction in gas temperature), the final volume of the mixture of hot gases and steam is less than the original volume of hot gases within the compartment.

The Key

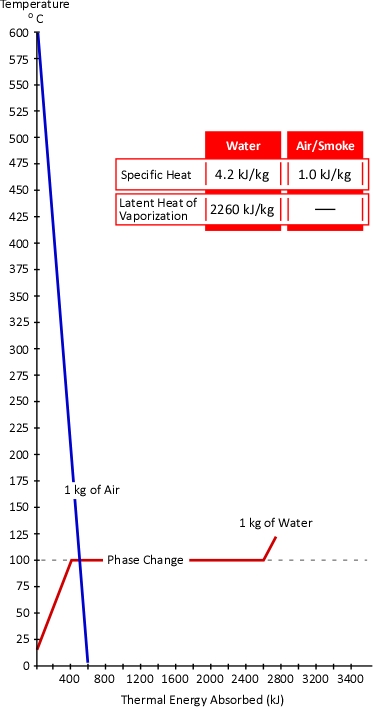
The temperature of the gases is lowered much more than the temperature of the water is increased. Why might this be the case? The key to this question lies in the concepts of specific heat and latent heat of vaporization. As illustrated in Figure 2, the specific heat of smoke is approximately 1.0 kJ/kg (Särdqvist, 2002; Yuen & Cheung, 1999) while the specific heat of water is 4.2 kJ/kg and even more importantly the latent heat of vaporization of water is 2260 kJ/kg. What this means is that it requires over four times the energy to raise the temperature of a kilogram of water by 1^o C than it does to lower the temperature of smoke by the same amount. In addition, it requires 2260 times the energy to turn 1 kg of water to steam at 100^o C than it does to lower the temperature of 1 kg of smoke by 1^o C.

Figure 2. Heating and Cooling Curves of Smoke & Water

While water expand as it turns to steam, the hot gas layer will contract as it’s temperature drops. At the same pressure, change in the volume of a gas is directly proportional to the change in absolute temperature. If the initial temperature of the hot gas layer is 500^o C (773 Kelvin) and its temperature is lowered to 100^o C (373 Kelvin) the absolute temperature is reduced by slightly more than half (773 K-373 K=400 K). Correspondingly the volume of the hot gases will also be reduced by half.

An Example

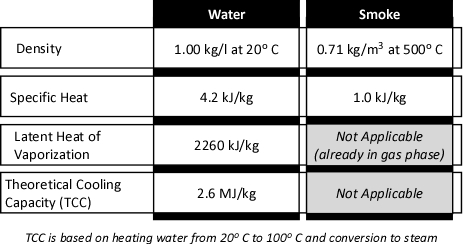
Once the underlying concept of gas cooling has been explained, the question of how a small amount of water can have such a dramatic effect may still remain. After all, the preceding explanation compared a kilogram of water to a kilogram of air. Firefighters normally do not usually think of either of these substances in terms of mass. Water is measured in liters or gallons. If measurement of smoke and air is thought of, it would likely be in cubic meters (m³) or cubic feet (ft³). Sticking with SI units, consider the properties of water and smoke as illustrated in Figure 3:

Figure 3. Properties of Water and Smoke

While over simplified, the compartment fire environment can be considered as being comprised of two zones; a hot upper layer and a cooler lower layer, each with reasonably uniform conditions (this is the approach used by computer models such as the Consolidated Model of Fire and Smoke Transport, CFAST).

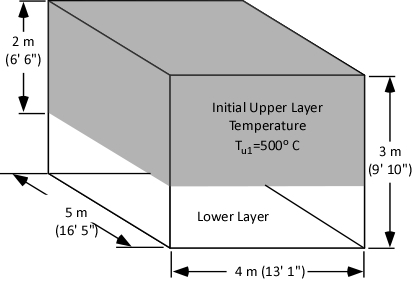
As illustrated in figure 4, our examination of gas cooling will consider a single compartment 4 meters (13’ 1”) wide and 5 meters (16’ 5”) long with a ceiling height of 3 meters (9’ 10”). The upper layer comprised of hot smoke and air is two meters deep and has an average temperature of 500^o C (932^o F).

Figure 4. Compartment with Two Thermal Zones

What volume of water must be applied into the upper layer to reduce its temperature from 500^o C to 100^o C?

Just as input of energy is required to increase temperature, energy must be transferred from a substance in order to lower its temperature. The first step in determining the water required for cooling is to calculate the energy that must be transferred from the upper layer to achieve the desired temperature reduction.

The specific heat of smoke is approximately 1.0 kJ/kg. This means that 1.0 kJ of energy must be transferred from a kilogram of smoke in order to reduce its temperature by 1^o C. This requires that we determine the mass of the upper layer.

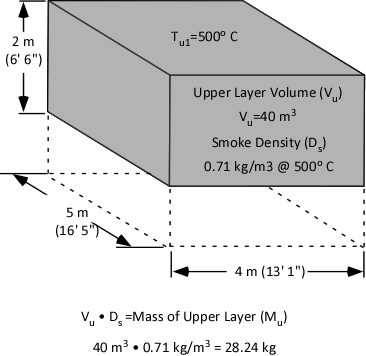
Calculation of mass involves multiplying the volume of the upper layer (40 m³) by the (physical) density of smoke (0.71 kg/m³) at the average temperature of the upper layer (500^o C) as illustrated in Figure 5.

Figure 5. Mass of the Upper Layer

Specific heat is the energy required to raise the temperature of a given unit mass of a substance 1^o. The same energy must be also be transferred to lower the temperature of a unit mass of a substance by 1^o. As illustrated in Figure 3, the specific heat of smoke is 1.0 kJ/kg. Therefore, to lower the temperature of a single kilogram of smoke by 1^o C, 1.0 kJ must be transferred from that kilogram of smoke. With an upper layer mass (Mu) of 28.24 kg, 28.24 kJ must be transferred from the upper layer to water applied for gas cooling in order to reduce its temperature by 1^o C.

Reduction of upper layer temperature from 500^o C to 100^o C is a change of 400^o. Multiplying 28.24 kJ by 400 determines the total amount of energy that must be transferred to water applied for gas cooling in order to reduce the temperature to 100^o C. As illustrated in Figure 6, 11,296 kJ (11.3 MJ) must be transferred from the upper layer to the water to effect a 400^o C reduction in temperature.

Figure 6. Energy Transfer Required

Now that we have determined the energy that must be transferred from the upper layer in order to lower the temperature from 500^o C to 100^o C, it is possible to identify how much water must be applied to accomplish this task. However, that will be the topic of my next post. In addition, I will provide an explanation as to why the volume of the upper layer does not (necessarily) increase when water applied to cool the gases turns to steam.

Ed Hartin, MS, EFO, MIFireE, CFO

References

Särdqvist, S. (2002). Water and other extinguishing agents. Karlstad, Sweden: Räddnings Verket.

Yuen, K. & Cheung, T. (1999). Calculation of smoke filling time in a fire room – a simplified approach. Journal of Building Surveying, 1(1), p. 33-37

Developing and maintaining proficiency in reading the Fire using the B-SAHF (Building, Smoke, Air Track, Heat, and Flame) organizing scheme for fire behavior indicators, requires practice. This post provides an opportunity to exercise your skills using a video segment shot during a commercial fire.

Commercial Fire

This post examines fire development during a fire in an agricultural facility in Spain. First arriving firefighters observed a small amount of light gray smoke issuing from roof ventilators and doorways with low velocity.

Download and the B-SAHF Worksheet.

Watch the first 50 seconds (0:50) of the video. First, describe what you observe in terms of the Building, Smoke, Air Track, Heat, and Flame Indicators; then answer the following five standard questions?

1. What additional information would you like to have? How could you obtain it?
2. What stage(s) of development is the fire likely to be in (incipient, growth, fully developed, or decay)?
3. What burning regime is the fire in (fuel controlled or ventilation controlled)?
4. What conditions would you expect to find inside this building?
5. How would you expect the fire to develop over the next two to three minutes

Now watch the next 20 seconds (1:10) of the video clip and answer the following questions:

1. Did fire conditions progress as you anticipated?
2. What changes in the B-SAHF indicators did you observe?
3. How do you think that the stage(s) of fire development and burning regime will change over the next few minutes?
4. What conditions would you expect to find inside this building now?
5. How would you expect the fire to develop over the next two to three minutes

Watch the remainder of the video. If you were the Incident Commander and had crews working inside the building, what information would you communicate to them as conditions change?

Reading the Fire

See the following posts for more information on reading the fire:

• Reading the Fire” How to Improve Your Skills
• Reading the Fire: Building Factors
• Reading the Fire Building Factors Part 2
• Reading the Fire: Building Factors Part 3
• Reading the Fire: Smoke
• Reading the Fire: Smoke Part 2
• Reading the Fire: Air Track
• Reading the Fire: Air Track Part 2
• Reading the Fire: Heat
• Reading the Fire: Heat Part 2
• Reading the Fire: Heat Part 3
• Reading the Fire: Flames
• Reading the Fire: Flames Part 2
• Reading the Fire: Putting it All Together
• Incipient Stage Fires: Key Fire Behavior Indicators
• Growth Stage Fires: Key Fire Behavior Indicators
• Fully Developed Fires: Key Fire Behavior Indicators
• Decay Stage Fires: Key Fire Behavior Indicators

Ed Hartin, MS, EFO, MIFIreE, CFO

My last two posts (Hazards Above, Hazards Above: Part 2)examined a series of incidents involving firefighter injuries or near miss incidents involving fires occurring in or extending into void spaces in wood frame, residential structures. Yesterday, two members of the Bridgeport, Connecticut Fire Department lost their lives under similar circumstances.

Bridgeport, CT LODD

At 1553 hours on Saturday, July 24, 2010, the Bridgeport, Connecticut Fire Department was dispatched for a residential fire at 41 Elmwood Avenue. First arriving companies found heavy smoke from Floors 2 and 3 of a 2-1/2 story, wood frame, multi-family dwelling. Lieutenant Steven Velazquez and Firefighter Michael Baik were performing a search of the third floor when they transmitted a Mayday. Lieutenant Velazquez and Firefighter Baik were located on Floor 3 by the Rapid Intervention Team (RIT), but were not breathing and in cardiac arrest when removed from the building. CPR was initiated and they were transported to Bridgeport and St. Vincent’s Hospitals where they were pronounced dead.

More information on this tragic incident will be provided as it becomes available.

FBI and Ventilation Controlled Fires-the UL Experiments

As discussed in Hazards Above: Part 2, obvious smoke and air track indicators of a ventilation controlled fire may become diminished as the fire transitions from growth to decay stage. The decay stage ventilation controlled fire may present similar (but not identical) indicators to an incipient or early growth stage fire.

Underwriters Laboratories (UL) recently conducted a study of the effects of horizontal, natural ventilation on fires in residential structures (see Did You Ever Wonder. The results of this research will be released this fall along with a free on-line training program through UL University. During this research 15 experiments were conducted in two different residential structures. Fuel loading was consistent and the point of origin was a couch in the living room for each of the tests. The variable was the location, size, and sequence of horizontal ventilation. Interestingly, one observation remained remarkably consistent throughout the tests: Diminished smoke and air track indicators as the ventilation controlled fire transitioned from growth to decay stage. This is illustrated by a series of screen captures from video shot from Side A of the one-story structure used in these experiments.

Figure 1. Early Growth Stage

Figure 2. Growth Stage (Peak HRR Prior to Ventilation)

Figure 3. Decay Stage (Reduced HRR)

Figure 4. Conditions Immediately Following Ventilation (HRR Increasing)

Another commonality between each of the experiments was a fairly rapid and significant increase in HRR after ventilation was performed. In no case did ventilation (alone) improve conditions at any location or level inside the test buildings. Horizontal, natural ventilation (tactical or unplanned) with a delay in application of water to the seat of the fire will result in worsening conditions.

Situational Awareness

As illustrated in Figure 3, lack of obvious indicators can be deceptive. The structure used in the UL tests did not have normal window glazing as this would have resulted in less predictability in the exact location and sequence of ventilation. However, in an actual structure fire, observation of smoke conditions through windows, condensation on window glazing (incipient or early growth stage) and condensed pyrolizate (decay stage), and heat effects on window treatments (e.g., curtains, blinds) can provide important cues related to the stage of fire development and burning regime.

It is critical to take a holistic approach to observation of fire behavior indicators, to begin this process from the exterior, and to continue this process while operating on the interior.

Ed Hartin, MS, EFO, MIFIreE, CFO

My last post, Hazards Above, provided a brief overview of three incidents involving extreme fire behavior in the attic or truss loft void spaces of wood frame dwellings. This post will examine the similarities and differences between these lessons and identify several important considerations when dealing with fires occurring in or extending to void spaces. At the conclusion of Hazards Above, I posed five questions:

1. What is similar about these incidents and what is different?
2. Based on the limited information currently available, what phenomena do you think occurred in each of the cases? What leads you to this conclusion?
3. What indicators might have pointed to the potential for extreme fire behavior in each of these incidents?
4. How might building construction have influenced fire dynamics and potential for extreme fire behavior in these incidents?
5. What hazards are presented by fires in attics/truss lofts and what tactics may be safe and effective to mitigate those hazards?

Similarities and Differences

The most obvious similarities between these incidents was that the buildings were of wood frame construction, the fire involved or extended to an attic or truss loft void space, and that some type of extreme fire behavior occurred. In two of the incidents firefighters were seriously injured, while in the other firefighters escaped unharmed.

Given the limited information available from news reports and photos taken after the occurrence of the extreme fire behavior events, it is not possible to definitively identify what types of phenomena were involved in these three incidents. However, it is interesting to speculate and consider what conditions and phenomena could have been involved. It might be useful to examine each of these incidents individually and then to return to examine fire behavior indicators, construction, and hazards presented by these types of incidents.

Minneapolis, MN

In the Minneapolis incident the fire occurred in an older home with legacy construction and relatively small void spaces behind the knee walls and above the ceiling on Floor 3. The triggering event for the occurrence of extreme fire behavior is reported to be opening one of the knee walls on Floor 3. As illustrated in Figure 1, the fire appeared to transition quickly to a growth stage fire (evidenced by the dark smoke and bi-directional air track from the windows on Floor 3 Side A. However blast effects on the structure are not visible in the photo and were not reported.

Figure 1. Minneapolis MN Incident: Conditions on Side A

Note: Photo by Steve Skar

Potential Influencing Factors: While detail on this specific incident is limited, it is likely that the fire burning behind the knee wall was ventilation controlled and increased ventilation resulting from opening the void space resulted in an increase in heat release rate (HRR). Potential exists for any compartment fire that progresses beyond the incipient stage to become ventilation controlled. This is particularly true when the fire is burning in a void space.

Extreme Fire Behavior: While statements by the fire department indicate that opening the knee wall resulted in occurrence of flashover, this is only one possibility. As discussed in The Hazard of Ventilation Controlled Fires and Fuel and Ventilation, increasing ventilation to a ventilation controlled fire will result in increased HRR. Increased HRR can result in a backdraft (if sufficient concentration of gas phase fuel is present), a vent induced flashover, or simply fire gas ignition (such as rollover or a flash fire) without transition to a fully developed fire.

Harrisonburg, VA

The Harrisonburg incident involved extreme fire behavior in Exposure D (not the original fire unit). The extreme fire behavior occurred after members had opened the ceiling to check for extension. However, this may or may not have been the precipitating event. As illustrated in Figure 2, as members prepare to exit from the windows on Floor 3 , Side C, flames are visible on the exterior at the gable, but it appears that combustion is limited to the vinyl siding and soffit covering. There are no indicators of a significant fire in Exposure D at the time that the photo was taken. However, it is important to remember that this is a snapshot of conditions at one point in time from a single perspective.

Figure 2. Harrisonburg, VA Incident: Conditions on Side C

Note: Photo by Allen Litten

Potential Influencing Factors: The truss loft was likely divided between units by a 1 hour fire separation (generally constructed of gypsum board over the wood trusses). While providing a limited barrier to fire and smoke spread, it does not generally provide a complete barrier and smoke infiltration is likely. Sufficient smoke accumulation remote from the original fire location can present risk of a smoke explosion (see NIOSH Report 98-03 regarding a smoke explosion in Durango, Colorado restaurant). Alternately, fire extension into the truss loft above an exposure unit can result in ventilation controlled fire conditions, resulting in increased HRR if the void is opened (from above or below).

Extreme Fire Behavior: Smoke, air track, and flame indicators on Side C indicate that the fire in the truss loft may not have continued to develop past the initial ignition of accumulated smoke (fuel). It is possible that smoke accumulated in the truss loft above Exposure B and was ignited by subsequent extension from the fire unit. Depending on the fuel (smoke)/air mixture when flames extended into the space above Exposure B ignition could have resulted in a smoke explosion or a less violent fire gas ignition such as a flash fire.

Sandwich, MA

In the Sandwich incident, the extreme fire behavior occurred shortly after the hose team applied water to the soffit. However, this may or may not have been the precipitating event. As illustrated in Figure 3, the fire transitioned to a fully developed fire (likely due to the delay in suppression as the injured members were cared for). Blast effects on the structure are obvious.

Figure 3: Sandwich, MA: Conditions on Sides C and D

Note: Photos by Britt Crosby (http://www.capecodfd.com)

Potential Influencing Factors: The roof support system in this home appears to have been constructed of larger dimensional lumber (rather than lightweight truss construction). In addition, it is likely that the attic void spaces involved in this incident were large and complex (given the size of the dwelling and complex roof line). It appears that at least part of the home had a cathedral ceiling. Fire burning in the wood framing around the metal chimney would have allowed smoke (fuel) and hot gases to collect in the attic void in advance of fire extension.

Extreme Fire Behavior: The violence of the explosion (see blast damage to the roof on Side D in Figure 3) points to the potential for ignition of pre-mixed fuel (smoke) and air, resulting in a smoke explosion. However, it is also possible that failure of an interior ceiling (due to water or steam production from water applied through the soffit) could have increased ventilation to a ventilation controlled fire burning in the attic, resulting in a backdraft).

Fire Behavior Indicators

The information provided in news reports points to limited indication of potential for extreme fire behavior. One important question for each of us is how we can recognize this potential, even when indicators are subtle or even absent.

Important! A growth stage fire can present significant smoke and air track indicators, with increasing thickness (optical density), darkening color, and increasing velocity of smoke discharge. However, as discussed in The Hazard of Ventilation Controlled Fires, when the fire becomes ventilation controlled, indicators can diminish to the point where the fire appears to be in the incipient stage. This change in smoke and air track indicators was consistently observed during the full-scale fire tests of the influence of ventilation on fires in single-family homes conducted by UL earlier this year.

Even with an opening into another compartment or to the exterior of the building, a compartment fire can become ventilation controlled. Consider building factors including potential for fire and smoke extension into void spaces in assessing fire conditions and potential for extreme fire behavior. A ventilation controlled fire or flammable mixture of smoke and air may be present in a void space with limited indication from the exterior or even when working inside the structure.

Building Construction

Each of these incidents occurred in a wood frame structure. However, the construction in each case was somewhat different.

In Minneapolis, the house was likely balloon frame construction with full dimension lumber. As with many other structures with a “half-story”, the space under the pitched roof is framed out with knee walls to provide finished space. This design is not unique to legacy construction and may also be found with room-in-attic trusses. The void space behind the knee wall provides a significant avenue for fire spread. When involved in fire, opening this void space can quickly change fire conditions on the top floor as air reaches the (likely ventilation controlled) fire.

The incident in Harrisonburg involved a fire in a townhouse with the extreme fire behavior phenomena occurring in an exposure. While not reported, it is extremely likely that the roof support system was comprised of lightweight wood trusses. In addition, there was a reverse gable (possibly on Sides A and C) that provided an additional void. As previously indicated, the truss loft between dwelling units is typically separated by a one-hour rated draft stop. Unlike a fire wall, draft stops do not penetrate the roof and may be compromised by penetrations (after final, pre-occupancy inspection). Installed to code, draft stops slow fire spread, but may not fully stop the spread of smoke (fuel) into the truss lofts above exposures.

Firefighters in Sandwich were faced with a fire in an extremely large, wood frame dwelling. While the roof appeared to be supported by large dimensional lumber, it is likely that there were large void spaces as a result of the complex roofline. In addition, the framed out space around the metal chimney provided an avenue for fire and smoke spread from the lower level of the home to the attic void space.

Hazards and Tactics

Forewarned is forearmed! Awareness of the potential for rapid fire development when opening void spaces is critical. Given this threat, do not open the void unless you have a hoseline in hand (not just nearby).

Indirect attack can be an effective tactic for fires in void spaces. This can be accomplished by making a limited opening and applying water from a combination nozzle or using a piercing nozzle (which further limits introduction of air into the void).

If there are hot gases overhead, cool them before pulling the ceiling or opening walls when fire may be in void spaces. Pulses of water fog not only cool the hot gases, but also act as thermal ballast; reducing the potential for ignition should flames extend from the void when it is opened.

Lastly, react immediately and appropriately when faced with worsening fire conditions. Review my previous posts on Battle Drill (Part 1, Part 2, and Part 3). An immediate tactical withdrawal under the protection of a hoseline is generally safer than emergency window egress (particularly when ladders have not yet been placed to the window).

Ed Hartin, MS, EFO, MIFireE, CFO

Finally! It has been quite some time since my last post, but the CFBT-US web site and blog have been attacked twice by hackers WordPress and ISP upgrade issues have been a major challenge and it has taken some time to get things back to normal.

A Big Improvement, But More Work is Needed

The Fire Service in the United States saw a considerable reduction in firefighter line-of-duty deaths in 2009. However, our efforts to improve firefighter safety must persist. Recent events reinforce the need to ensure understanding of practical fire dynamics and have the ability to apply this understanding on the fireground.

Three recent incidents involving extreme fire behavior present an opportunity to examine and reflect on the hazards presented by fires and accumulation of excess pyrolizate and unburned products of combustion in attics and other void spaces.

Minneapolis, MN Residential Fire

At 1130 hours on Saturday, July 3, 2010 Minneapolis firefighters responded to a residential fire at 1082 17th Avenue SE. First arriving companies observed light smoke and flames showing from a two and one-half story wood-frame home. A crew opening up the kneewall on the A/D corner of Floor 3 was trapped on the third floor by rapid fire progress.

Note: Photo by Steve Skar

A department spokesperson indicated that as they opened up the walls “it flashed over on them”. News reports indicated that the blast threw Firefighter Jacob LaFerriere, across the room and that he was able to locate a window, where he exited and dropped to the porch roof, one floor below. Capt. Dennis Mack was able to retreat into the stairwell where he was assisted to the exterior by other crews operating on the fireground (Mathews, 2010; Radomski & Theisen, 2010).

News reports also reported that a witness stated that the “flashover was quite loud and within seconds heavy fire was venting from the attic area” (Mathews, 2010). A later statements by department spokespersons indicated introduction of oxygen when the wall was opened resulted in the flashover (Porter, 2010) and that a burst of flames blew out the south side of the roof (Radomski & Theisen, 2010).

Firefighter Jacob LaFerriere suffered third degree burns on his arms and upper body. Capt. Dennis Mack suffered second degree burns (Radomski & Theisen, 2010) and are as of Sunday, July 4 were in satisfactory condition in the Hennepin County Medical Center Burn Unit.

Harrisonburg, VA Townhouse Fire

On June 24, 2010 Harrisonburg, Virginia firefighters responded to an apartment fire off Chestnut Ridge Drive. First arriving companies encountered a fire in a townhouse style, wood frame apartment. Investigating possible extension into Exposure Bravo, Firefighters Chad Smith and Bradly Clark observed smoke and then flames in the attic. They called for a hoseline, but when the pulled the ceiling, conditions worsened as the room ignited. Both firefighters escaped through a second floor window (head first, onto ladders placed by exterior crews). Four other firefighters were inside Exposure B when the extreme fire behavior occurred. Two received second degree burns, one was treated for heat exhaustion, and the fourth was uninjured (Firehouse.com News, 2010; WHSV, 2020). Department spokespersons indicated that a backdraft occurred when fire gases built up in the attic.

Note: Photo by Allen Litten

Sandwich MA Residential Fire

At around noon on Memorial Day, Sandwich, Massachusetts firefighters responded to a residential fire at 15 Open Trail Road. On arrival they found a 5,000 ft² (464 m²) wood frame single-family dwelling with a fire on Side C (exterior) with extension into the home. Firefighters Daniel Keane and Lee Burrill stretched a handline through the door on Side A, knocking down the fire and extending the line out onto a deck on Side C. Fire was extending through a void containing a metal chimney flue on the exterior of the building. The crew on the hoseline was making good progress until they hit the soffit with a straight stream and an explosion occurred. The force of the blast knocked the crew over the deck railing and caused significant structural damage. Firefighter Keane suffered fractures of his neck and back while Firefighter Burrill experienced a severely fractured ankle (Fraser, 2010; D LeBlanc personal communication June 2010).

Note: Photos by Britt Crosby (http://www.capecodfd.com/)

Questions

One of these fires occurred in an older home of legacy construction, the other two occurred in relatively new buildings. One was a large contemporary home, likely with an open floor plan and large attic/trussloft voids. The other two occurred in buildings with smaller void spaces in the attic/trussloft.

1. What is similar about these incidents and what is different?
2. Based on the limited information currently available, what phenomena do you think occurred in each of the cases? What leads you to this conclusion?
3. What indicators might have pointed to the potential for extreme fire behavior in each of these incidents?
4. How might building construction have influenced fire dynamics and potential for extreme fire behavior in these incidents?
5. What hazards are presented by fires in attics/trusslofts and what tactics may be safe and effective to mitigate those hazards?

Late Breaking Information

Two firefighters and an officer from the Wharton Fire Department were trapped by rapid fire progress in a commercial fire at the Maxim Production Company in Boling, TX on July 3, 2010. The crew had advanced a hoseline into the 35,000 ft² (3252 m²) egg processing plant to cut off fire extension when they encountered rapidly worsening fire conditions. The two firefighters were able to escape, but Captain Thomas Araguz III was trapped and killed (Statter, D., 2010). More information will be provided on this incident as it becomes available.

References

Mathews, P. (2010). Two Minn. ffs burned in flashover. Retrieved July 4, 2010 from http://www.firehouse.com/news/top-headlines/two-minneapolis-firefighters-burned-flashover

Radomski, L & Theisen, S. (2010). Firefighters hospitalized after flashover identified. Retrieved July 4, 2010 from http://kstp.com/news/stories/S1637495.shtml?cat=1

Porter, K. (2010). 2 firefighters burned in Mpls. fire ID’d. Retrieved July 5, 2010 from http://www.kare11.com/news/news_article.aspx?storyid=856556&catid=396

WHSV. (2010) Harrisonburg firefighters talk about their close call. Retrieved July 5, 2010 from http://www.whsv.com/home/headlines/97127924.html

Firehouse.com News. (2010). Harrisonburg, Va. firefighters forced to bail out. Retrieved July 5, 2010 from http://www.firehouse.com/showcase/photostory/harrisburg-va-firefighters-have-bail-out

Fraser, D. (2010). Mass. firefighters thrown more than 30 Ft. by blast. Retrieved July 5, 2010 from http://www.firehouse.com/news/top-headlines/blast-throws-mass-firefighters-more-30-feet

Statter, D. (2010). Update: Captain Thomas Araguz III killed during 4-alarm fire at egg plant in Boling, Texas. http://statter911.com/2010/07/04/firefighter-killed-during-4-alarm-fire-at-egg-plant-details-from-wharton-county-texas/

Last night I returned from The International Fire Instructors Workshop and OTTAWA FIRE 2010 Symposium. The workshop was started in 2008 by Dr. Stefan Svensson of the Swedish Civil Contingency Agency who wanted to see what would happen if he put a number of operational fire officers, instructors, scientists and engineers, in a room together for discussion of ideas of mutual interest. Since then, the workshop has continued to provide a forum for a loosely organized network of operational firefighters and fire officers, engineers, and scientists with a passionate interest in fire dynamics and firefighting. However, despite the looseness of our organization, we have had a tremendous impact on one another and continue efforts to positively influence our respective fire services understanding of fire dynamics.

OTTAWA FIRE 2010

At the closing of OTTAWA FIRE 2010 symposium, our host, and symposium organizer, Captain Peter McBride of Ottawa Fire Services rephrased the oft repeated sentiment that the fire service has seen 100 (or more) years of tradition, unimpeded by progress. He stated that the symposium was five days of progress, unimpeded by tradition. As stated on the symposium web site:

The OTTAWA FIRE 2010 symposium was conceived to address the needs of Ottawa Fire Services personnel in response to the recommendations of the Workers’ Report on Critical Injuries as a result of the Forward Avenue Fire on February 12, 2007.

Over the last week, the Ottawa Professional Firefighters Association in partnership with the Ottawa Fire Services, the National Research Council of Canada and Carleton University’s Industrial Chair in Fire Safety Engineering hosted this international symposium which was held in Ottawa at Carleton University. The partners sought to examine the issues facing the fire service through relationships, education, discovery and advocacy. This effort was a rousing success!

Purposeful Action

Firefighter Carissa Campbell-Darmody opened the symposium with a presentation entitled First One Out, giving a first person account of her traumatic experience in the Forward Avenue fire. On February 12, 2007 the members of Ottawa Fire Services Station 11, D Platoon (Pumps 11A, 11B, and Ladder 11) responded to a reported structure fire at 187 Forward Avenue. Within 9 minutes, they would be fighting to survive wind driven rapid fire progression that cut off their means of escape from the third floor of an apartment building.

Note: Photo by Jean Ladonde from Workers Report Critical Injuries: Forward Avenue Fire Ottawa Fire Services Incident # 07-8038, February 2007.

Three members of Pump 11B (Lieutenant John Chatterton, Firefighter Robert Witham and Probationary Firefighter Carissa Campbell) were trapped on the third floor of Exposure Delta while conducting primary search. Two members of Ladder 11 (Lieutenant Tim Taylor and Firefighter Gerald Barrett) were trapped on the third floor of the fire unit after rescuing an occupant and continuing primary search operations. All of these members were forced to jump from the third floor (fourthlevel including basement which was substantively above grade) to escape untenable conditions and suffered burns and musculoskeletal trauma.

As with most investigations into significant injuries or fatalities, the Workers’ Investigation conducted by the Ottawa Professional Firefighters Association identified multiple causal and contributing factors related to the tragic outcome of this incident.

Carissa’s presentation of the sequence of events and the experiences of her crew during this incident were incredibly detailed, insightful, and provided a powerful focus for the purpose of the symposium.

Connections

The symposium included a wide range of presentations focused on the importance of science and engineering to the firefighters’ work. Of particular significance were discussion of Managing the Mayday by Battalion Chief George Healy of the Fire Department of the City of New York (FDNY), Understanding the Fire Environment and Ventilating Today’s Residential House Fires by Steve Kerber from Underwriters Laboratories (UL), Wind Driven Fires by Dan Madryzkowski from the National Institute for Standards and Technology (NIST) and a historical look at the evolution of Ventilation Tactics by Battalion Chief Gerry Tracy of FDNY (retired).

Symposium participants also had the opportunity to observe how scientific research impacts the fire service with a visit to the Canadian National Research Council’s fire research facility.

Quantitative and Qualitative Research

On the last day of the symposium, I delivered a presentation on the use of case studies which emphasized the importance of both quantitative and qualitative research to the fire service. As frequent readers of this blog are aware, case studies can be a useful method of gaining insight into both the events involved in a particular event as well as identifying commonality with similar events. This presentation will be incorporated into several subsequent posts.

Ed Hartin, MS, EFO, MIFireE, CFO

References

Ottawa Professional Firefighters Association, International Association of Firefighters Local 162. (2007). Workers Report Critical Injuries: Forward Avenue Fire Ottawa Fire Services Incident # 07-8038, February 2007. Retrieved May 23, 2010 from http://www.ottawafirefighters.org/ottawafire2010/docs/ForwardAvenue_24_01_10.pdf

As a critical friend of the NIOSH Firefighter Fatality Investigation and Prevention Program, I have provided testimony at public hearings and engaged in discussions with NIOSH staff regarding improvement of the quality of information provided in Death in the Line of Duty Reports, particularly in incidents involving extreme fire behavior. In addition, I have provided expert review on a number of Death in the Line of Duty Reports (including F2009-11). The discussion of fire dynamics, fire behavior indicators, and influence of ventilation and wind effects in Report F2009-11 is evidence that this feedback has been heard! I would like to thank Tim Merinar and the other NIOSH staff for their efforts in this area.

However, more work is needed. Just over a year ago, I read a news report about the deaths of Captain James Harlow and Firefighter Damion Hobbs of the Houston Fire Department during operations at a residential fire. I recalled Houston had seen a number of fatalities during structural firefighting over a reasonably short period of time. Curious, I reviewed reports on these incidents developed by NIOSH and the Texas State Fire Marshal�s Office. Seeing some commonality in the circumstances surrounding these incidents, I called a colleague at NIOSH and recommended that the investigation of the incident in which Captain Harlow and Firefighter Hobbs lost their lives, include review of prior incidents (and near miss data if available) to identify underlying causal or contributing factors that may not be evident from examination of a single incident.

While we often want to know the cause of a tragic event, the reality is that it is often much more complicated that we would like. Investigative reports such as those prepared by NIOSH focus a bright light on the what and how, but often leave the question of why hidden in the shadows. Observations and questions in this post are not presented as an indictment of the Houston Fire Department, or to question the commitment and bravery of Captain Harlow and Firefighter Hobbs, but simply to encourage each and every one of us to look more deeply; more deeply at our profession, at our own organizations, and at ourselves.

Epidemiology

Epidemiology is the study of factors affecting the health and illness of populations. Epidemiological research is the foundation of public health intervention and preventative medicine. This research is focused at identifying relationships between exposures and disease or death. Identification of causal relationships between exposures and outcomes is critical. However, correlation does not determine cause, and identification of causality is often complex and tentative.

For the fire service, epidemiological study has and continues to focus on heart disease, stress, and cancer (see USFA, NIOSH Launch Cancer Study). However, these same concepts can be applied to traumatic fatalities as well.

R-Fire 7811 Oak Vista, Houston TX

On April 12, 2009 Captain James Harlow and Firefighter Damion Hobbs lost their lives in a residential fire at 7811 Oak Vista in Houston, Texas. On April 9, 2010, the National Institute for Occupational Safety and Health released Death in the Line of Duty Report F2009-11 summarizing their investigation of this incident. Overall, this report is well written and provides an excellent examination of the events involved in this incident. The Texas State Fire Marshal�s Office also conducted an investigation of this incident and released a report a short time prior to release of NIOSH Report F2009-11.

• NIOSH Death in the Line of Duty F2009-11
• Texas State Fire Marshal�s Office Firefighter Fatality Investigation FY09-01

Contributing Factors

NIOSH identified eight items as key contributing factors in the deaths of Captain Harlow and Firefighter Hobbs:

• An inadequate size-up prior to committing to tactical operations
• Lack of understanding of fire behavior and fire dynamics
• Fire in a void space burning in a ventilation controlled regime
• High winds
• Uncoordinated tactical operations, in particular fire control and tactical ventilation
• Failure to protect the means of egress with a backup hose line
• Inadequate fireground communications
• Failure to react appropriately to deteriorating conditions.

What is missing from this list? Six of the seven items on this list relate to human action or inaction. The report points out the need for policy, procedures, and additional training to address the contributing factors. While this is undoubtedly necessary, does this provide the entire answer?

The Remaining Question

As with all NIOSH firefighter fatality investigations, the focus of this report is on the circumstances and events surrounding a single incident. In this report, there is a brief mention of investigation of the deaths of other firefighters from this department, but no analysis of commonality or underlying contributing factors is provided. This leaves the question, to what extent did organizational culture impact on the circumstances and events involved in this tragic incident?

In his keynote presentation at the 2010 Fire Department Instructor�s Conference, Lieutenant Frank Ricci of the New Haven (CT) Fire Department indicated that the culture of the fire service is wrongly blamed for many of it�s problems. Lieutenant Ricci indicated that a large percentage of firefighter injuries and deaths are not due to inherent risks, but to an �unwillingness to take personal responsibility for safety� (Thompson, 2010). I would ask, why are firefighters unwilling to take personal responsibility? What factors influence this pattern of behavior? I suspect that it is our unquestioned assumptions about the way that things are (part of our culture). In this sense, culture is not to blame, but is simply one of a number of contributing and causal factors in many firefighter fatalities.

Common Elements

A cursory examination of the facts presented in the reports of NIOSH investigation of traumatic fatalities in the Houston Fire Department since 2000 shows a distinct pattern. Each of the fatalities involved members of the first arriving company where a fast attack was initiated without adequate size up and in most (and likely all) cases failure to assess risk versus gain. A more detailed examination of these events would likely provide a more finely grained picture of organizational expectations that make extremely aggressive fire attack without adequate size-up and risk assessment the norm, rather than the exception.

Table 1. Traumatic Line-of-Duty-Deaths in Houston, Texas 2000-2009

A Comparison

On September 11, 1991, Continental Express Flight 2574 crashed in Eagle Lake Texas killing all 14 people aboard. As with all commercial aircraft accidents, this incident was investigated by the National Transportation Safety Board.� The board identified the cause as failure of maintenance and inspection personnel to adhere to proper maintenance and quality assurance procedures. However, the board also identified failure of management to ensure compliance with approved procedures and failure of Federal Aviation Administration to detect and correct this problem as contributing factors. Board member John K. Lauber, filed a dissenting statement. �It is clear based on this record alone, that the series of failures which led directly to the accident were not the result of an aberration, but rather resulted from the normal accepted way of doing business at Continental Express� (NTSB, 1992, p. 53). Lauber advocated restating the probable cause of this accident as �the failure of Continental Express management to establish a corporate culture which encouraged and enforced adherence to approved maintenance and quality assurance procedures� (NTSB, 1992, p. 54).

It is essential to look at the five events identified in reports F2000-13, F2001-33, F2004-14, F2005-09, and F2009-11 (NIOSH, 2001, 2002, 2005a, 2005b, 2010) from a longitudinal perspective to identify in greater detail and understand the common elements and potential systemic cultural issues that influenced the actions of those involved. While the influence of organizational culture is more difficult to identify than failure to comply with good practice, failure to recognize a hazardous condition, or an error in decision-making, it has a far more pervasive influence on fire fighter safety than these specific, individual acts.

Based on limited research, it is apparent that the Houston Fire Department (like many others) places an extremely high value on rapid and aggressive offensive firefighting operations. While the outcome of this incident resulted from a wide range of interrelated contributing factors, organizational culture and lack of knowledge regarding fire behavior and the influence of tactical operations were likely the most significant.

Identification of organizational culture as a contributing factor in this incident is based on data included in the DRAFT report as well as review of NIOSH Reports F2000-13, F2001-33, F-2004-14, F2005-09, and F2009-11 (NIOSH, 2001, 2002, 2005a, 2005b, 2010) as well as review of the Houston Fire Department Strategic Plan FY2008-2012 (n.d., HFD) and Philosophy of Firefighting (2003, HFD).

A memorandum from the Office of the Fire Chief defining the Houston Fire Department�s philosophy of firefighting (HFD, 2003) after the McDonald�s (NIOSH, 2001) and Four Leaf Tower (NIOSH, 2002) fires reinforced the importance of risk assessment in selecting strategies and tactics. In this memo, the chief identified the importance of organizational culture, stating �we pride ourselves in being very aggressive interior fire fighters and look down on those that fight fire from the street� (p. 1). While this memorandum was written in 2003, lack of adequate size up and risk assessment was a contributing factor in three incidents resulting in four line-of-duty deaths involving Houston Fire Department members in subsequent six years.

The Houston Fire Department Strategic Plan for FY2008-2012 (n.d., HFD) identifies safety as a core organizational value, stating: �preservation of life remains the number one goal of the HFD beginning with the responder and extending to the public� (p. 5). This focus continues with enhancement of the health and safety of HFD members as the first goal within the strategic plan. However, while the strategic plan provides a detailed blueprint for action, no objective or action plan element addresses the predominant contributory factors that are common in the seven line-of-duty deaths of Houston Fire Department members resulting from traumatic cause between 1999 and 2009. For example, Objective 1.5 of the strategic plan focuses on National Fallen Fire fighter Initiative #1 which states �define and advocate the need for cultural change within the fire service relating to safety; incorporating leadership, management, supervision, accountability and personal responsibility (HFD, n.d., p. 8). However, the sub elements of this objective focus on near miss reporting, roadway emergency safety, and response to violent incidents.

In the incident that took the lives of Captain Harlow and Firefighter Hobbs, several elements point to the focus on speed and aggressive action. Despite his seniority and experience, the captain of the first arriving engine quickly initiated an interior attack without adequate size-up and risk assessment (or performed a size-up and failed to recognize critical fire behavior indicators). In addition, he left his portable radio on the apparatus, E-26s thermal imaging camera (TIC) was left outside the front door. Any one of these elements alone might indicate a simple error, but in combination along with the context provided by previous LODD incidents (NIOSH, 2001, 2002, 2005a, 2005b) this is likely evidence of the cultural value of speed and aggressive action over deliberate assessment of conditions and decision-making based on risk assessment.

While increased protection through the use of the reed hood has significant potential benefits (similar technology is used by the Swedish fire service), it is quite possible that this type of personal protective clothing (which is somewhat unique to the Houston Fire Department) is used to permit fire fighters to penetrate deeper into hostile environments, rather than simply to provide improved protection with the ordinary or hazardous range of conditions encountered during structural firefighting.

Recommendation

Based on these factors identified in NIOSH Report F2009-11 (2010) as well Reports F2000-13, F2001-33, F2004-14, F2005-09 (2001, 2002, 2005a, 2005b), I recommend that fire service organizations assess the impact of their organizational culture on fire fighter safety and operational performance.

Note that this recommendation is not simply focused on the Houston Fire Department. It is a global recommendation, that each of us examine the influence of culture within our respective organizations.

Ed Hartin, MS, EFO, MIFireE, CFO

References

Houston Fire Department. (2003) Philosophy of firefighting. Retrieved January 24, from http://www.houstontx.gov/fire/reports/philoff.pdf

Houston Fire Department. (n.d.) Houston Fire Department Strategic Plan FY2008-2012. Retrieved January 24 from http://www.houstontx.gov/fire/reports/SP0811.pdf

National Transportation Safety Board (NTSB). Aircraft accident report: Britt Airways, Inc. d/b/a/ Contenental Express Flight 2474 in flight structural breakup, EMB-120RT, N33701, Eagle Lake, Texas, September 11, 1991, NTSB/AAR-92/04. Washington, DC: Author.

National Institute for Occupational Safety and Health (NIOSH). (2001). Death in the line of duty, Report F2000-13. Retrieved January 24, 2010 from http://www.cdc.gov/niosh/fire/pdfs/face200013.pdf.

National Institute for Occupational Safety and Health (NIOSH). (2002). Death in the line of duty, Report F2001-33. Retrieved January 24, 2010 from http://www.cdc.gov/niosh/fire/pdfs/face200133.pdf.

National Institute for Occupational Safety and Health (NIOSH). (2005a). Death in the line of duty, Report F2004-14. Retrieved January 24, 2010 from http://www.cdc.gov/niosh/fire/pdfs/face200414.pdf.

National Institute for Occupational Safety and Health (NIOSH). (2005b). Death in the line of duty, Report F2005-09. Retrieved January 24, 2010 from http://www.cdc.gov/niosh/fire/pdfs/face200509.pdf.

National Institute for Occupational Safety and Health (NIOSH). (2010). Death in the line of duty, Report F2009-11. Retrieved April 25, 2010 from http://www.cdc.gov/niosh/fire/pdfs/face200911.pdf

Thompson, J. (2010) FDIC keynote: Fire service culture not to blame for problems. Retrieved May 3, 2010 from http://www.firerescue1.com/firefighter-safety/articles/810852-FDIC-keynote-Fire-service-culture-not-to-blame-for-problems/

It has been a number of months since the last Reading the Fire post. It is essential to continue the process of deliberate practice in order to continue to improve and refine skill in Reading the Fire.

As we start the New Year it is a good time to reaffirm our commitment to mastering our craft. Developing and maintaining proficiency in reading the Fire using the B-SAHF (Building, Smoke, Air Track, Heat, and Flame) organizing scheme for fire behavior indicators, requires practice. This post provides an opportunity to exercise your skills using a video segment shot during a residential fire.

Residential Fire

In mid-January 2010, the Gary, Indiana Fire Department was dispatched to a residential fire on Massachusetts Street at East 24^th Avenue, on arrival Battalion 4 advised of a working fire in a 2 story dwelling. While the first arriving engine was laying a supply line from a nearby hydrant, the first in truck forced entry.

Download and the B-SAHF Worksheet.

Watch the first 35 seconds (0:35) of the video. This segment was shot from Side A. �First, describe what you observe in terms of the Building, Smoke, Air Track, Heat, and Flame Indicators; then answer the following five standard questions?

1. What additional information would you like to have? How could you obtain it?
2. What stage(s) of development is the fire likely to be in (incipient, growth, fully developed, or decay)?
3. What burning regime is the fire in (fuel controlled or ventilation controlled)?
4. What conditions would you expect to find inside this building? If presented with persons reported (as the first arriving companies were) how would you assess potential for victim survival?
5. How would you expect the fire to develop over the next two to three minutes

Now watch the remainder of the video clip and answer the following questions:

1. Did fire conditions progress as you anticipated?
2. A voice heard in the video states that this was a backdraft. Do you agree? Why or why not?

It is likely that the first in truck company in this incident made entry to search for occupants and to locate the fire. Regardless of your perspective on search with or without a hoseline, this video clip provides lessons.

• It is essential to read the fire, recognize the stage(s) of fire development and burning regime(s) in the involved compartments.
• In addition to reading current conditions, anticipate likely fire development and potential for extreme fire behavior.
• Making entry (and leaving the door fully open) creates a ventilation opening (inlet, exhaust, or both). Recognize the potential influence of changes to the ventilation profile on fire behavior.
• To borrow a phrase from a number of National Institute for Occupational Safety and Health Death in the Line of Duty reports; �Ventilation and fire attack must be closely coordinated�. One key element in this coordination is that charged lines must be in place before completion of ventilation openings. This is critical when dealing with a ventilation controlled fire.

Ed Hartin, MS, EFO, MIFIreE, CFO

Firefighters are often provided with an oversimplified explanation of fundamental scientific concepts related to fire behavior. This is done with the intent to make training manuals and texts understandable and to focus on the information that firefighters �must know�. However, a tremendous opportunity to develop the ability to make sense of fire dynamics and the impact of tactical operations is lost in the process. This series of posts continues to explore ways of building a scaffold to allow firefighters to develop a deeper understanding of firefighting as science.

Electromagnetic Radiation

The term radiation is used to describe many different things ranging from visible light, infrared light, and ionizing radiation such as x or gamma rays. Each of these is an example of radiation as an electromagnetic wave produced by the motion of electrically charged particles. Electromagnetic radiation can travel through empty space and air. Radiation can also penetrate through other materials depending on the characteristics of the material and the radiation�s energy. Some ionizing radiation is in the form of particles (rather than waves), but that is outside the scope of our examination of radiation as a mechanism of heat transfer.

As illustrated in Figure 1, electromagnetic waves can be described in terms of their wavelength, amplitude, frequency, and energy.

Most of the electromagnetic spectrum cannot be detected by the human eye. While the electromagnetic spectrum includes radiation in a broad range of wavelengths, those of most interest in the study of fire behavior are categorized as infrared

Figure 1. Electromagnetic Wave

From longest to shortest wavelengths, the spectrum is usually divided into the following sections: radio, microwave, infrared, visible, ultraviolet, x-ray, and gamma-ray radiation. Humans can only see a narrow band of visible light, which is a small fraction of the electromagnetic spectrum. We perceive this radiation as the colors of the rainbow ranging from red to violet, with reds having longer wavelengths �and violet having shorter wavelengths

Thermal radiation is electromagnetic radiation emitted from the surface of an object which is due to the object’s temperature. Any material that is above absolute zero gives off some radiant energy. Thermal radiation is generated when heat from the movement of charged particles within atoms is converted to electromagnetic radiation.

Figure 2. Electromagnetic Spectrum

Figure 3. Planck’s Curve

Thermal radiation occurs at a wide range of frequencies. However, as illustrated in Figure 2, the power emitted at each wavelength is dependent on temperature, with the main frequency and power of emitted radiation increasing as temperature increases. This can be observed when color changes from red, to yellow, and then white as an object is heated. While color change is visible, most of the radiant energy is still in the infrared spectrum.

Electromagnetic waves of any frequency will heat surfaces that absorb them. However, temperatures of hot surfaces, gases, and flames in the fire environment result in emission of electromagnetic waves predominantly in the infrared and visible portion of the spectrum.

Stefan-Boltzmann Law: The amount of energy per square meter per second that is emitted by a black body is related to the fourth power of its Kelvin temperature. As temperature increases, emission of radiant energy increases exponentially.

A black body is a theoretical object that completely absorbs all incoming radiant energy and is also a perfect emitter of radiant energy. Materials encountered in the fire environment do not completely have the characteristics of a black body and may be classified as gray bodies. A gray body absorbs or emits a portion of the radiative flux depending on the emissivity (?).

Emissivity is the relative ability of the surface of a material to emit radiant energy. It is the ratio of energy radiated by a particular material to energy radiated by a black body at the same temperature. Emmisivity of a black body would be 1.0 with the emissivity of actual materials ranging from approximately 0.1 for highly reflective materials (e.g., polished silver) to 0.97 for fairly efficient absorbers and emitters of radiant energy (e.g., carbon particulate).

Emission of radiant energy is measured as heat flux (energy transfer per unit of time over a given surface area). The SI unit of measure is joules/second/square meter or (since a watt is a J/s) watts/square meter (w/m²).

Figure 4. Stefan Boltzmann Law

Electromagnetic radiation spreads out as it moves away from its source. As a result, the intensity of the radiation decreases as distance from the source becomes greater (as illustrated in Figure 5). The simplest example involves a point source of radiation (distance from the source is much greater than the size (e.g. surface area) of the emitter). With a point source, reduction in radiation intensity follows the inverse square law.

Figure 5. Radiation Intensity Decreases With Distance

Inverse Square Law: For point sources, intensity of the radiation varies inversely with the square of the distance from the source. Doubling the distance reduces intensity of the radiation by a factor of four (1/4 of its original value).

When radiation is emitted from other than a point source (as it is under fire conditions), variation of the radiation intensity with distance is more complex. If the area of the source is large compared with the distances involved, intensity decreases with distance but does not follow a simple law. As a rough guide, if the distance from the source is greater than about 5 times the dimensions of the source, the inverse square law can be applied.

More to Follow

Subsequent posts in this series will examine physical and chemical changes and the process of combustion.

Ed Hartin, MS, EFO, MIFireE, CFO

Things to Think About

Methods of heat transfer are often presented to firefighters in a simplistic way with the expectation that they will understand the basic concepts and are assessed on their ability to recall the definitions of conduction, convection, and radiation. Unfortunately this does not provide a solid basis for understanding phenomena encountered on the fireground.

Convection

In general terms, convection refers to movement of molecules within fluids (i.e., liquids and gases). Convection results in both heat and mass transfer (these are interrelated as extensive properties such as thermal energy are dependent on mass). Convection involves diffusion due to random movement of individual molecules (Brownian motion) and large scale motion of currents in the fluid (advection).

Natural Convection

Natural or free convection results from temperature differences within a fluid. As a fluid is heated, it expands while mass remains the same. Decreased density (mass/unit volume) makes the heated fluid more buoyant, causing it to rise. As the heated fluid rises, cooler fluid flows in to replace it. Natural convection is one of the major mechanisms of heat transfer in a compartment fire, heated air and smoke rise and cooler air moves in to replace it. This process transfers thermal energy, heating other materials in the compartment and also transfers mass as smoke moves out of the compartment and cool air (containing oxygen necessary for continued combustion) moves into the compartment.

In the late 1700s, French scientist Jacques Charles studied the effect of temperature on a sample of gas at a constant pressure. Charles, found that as the gas was heated, the volume increased. As the gas was cooled, the volume decreased. This finding gave rise to Charles Law.

Charles’ Law: At a constant pressure, the volume occupied by a fixed mass of gas is directly proportional to its thermodynamic temperature (V?T).

Figure 1. Charles Law

Density is mass per unit volume (?=m/V). As the volume of a given mass of gas increases, it becomes less dense (and more buoyant). If unconfined, gases that are less dense than the surrounding air will rise (resulting in natural convection currents). In a compartment fire, conditions are not as simple as stated in Charles Law. Initially, hot gases resulting from a fire in a compartment are relatively unconfined as the volume of smoke and hot gases is small in relation to the size of the compartment and there may be some leakage of smoke from the enclosure. However, as the fire continues to develop, the volume of smoke increases and conditions change.

Gay-Lussac�s Law: At a constant volume and mass, the pressure exerted by a gas is directly proportional to its thermodynamic temperature (P?T).

The pascal (Pa) is the standard international unit of measure for pressure (force per unit area) and is defined as one newton per square meter (N/m²). To provide a point of reference for firefighters more familiar with pounds per square inch (psi) as a unit of measure for pressure, 1 Pa = 0.000145 psi. Low pressures (such as the pressure generated by temperature increases in a compartment fire) are measured in Pa while higher pressures (such as fire pump discharge pressure) are more commonly measured in kilopascals (kPa=1000 Pa).

As illustrated in Figure 2, if the volume is constant (e.g., the gas is confined) doubling the temperature in Kelvins, doubles the pressure in pascals (Pa).

Figure 2. Gay-Lussac’s Law

When a fire is unconfined (e.g., outdoors), convection is influenced primarily by differences in density between hot fire gases and cooler air. Convection as a result of a fire in an enclosure (e.g., compartment fire) is significantly influenced by differences in density and differences in pressure.

Figure 3. Natural Convection

Forced Convection

In forced convection, energy is carried passively by fluid motion which occurs independent of the heating process.

While at first glance, it may appear that this type of convection would not be encountered in the fire environment, but it is extremely important. Forced convection can be caused by natural effects such as wind blowing into an opening (e.g., window broken due to fire effects). This type of forced convection can quickly create untenable conditions both inside the compartment and in adjacent spaces (e.g., rooms, hallways). Forced convection can also have a positive influence on the fire environment. One example would be the use of positive pressure ventilation, in which a blower (fan) is used to create an air flow from an inlet to an exhaust opening, removing hot smoke and gases from the compartment.

Figure 4. Forced Convection/Wind Driven Fire

Note: Adapted from Fire Fighting Tactics Under Wind Driven Fire Conditions: 7-Story Building Experiments.

Factors Influencing Convective Heat Transfer

Heat transfer by convection is more complex than conduction as there is no single property such as thermal conductivity that can be used to describe the mechanism of heat transfer. Factors that influence heat transfer by convection in the fire environment include temperature difference between the fluid (gas) and surfaces, fluid velocity, and turbulence (related to surface roughness and compartment configuration).

Figure 5 illustrates convective heat transfer with laminar (smooth) fluid flow. Energy is transferred from higher temperature fluid molecules to the cooler surface. Bulk fluid temperature (T_b) is the temperature of the fluid some distance away from the surface. As heat is transferred, the temperature of the fluid molecules is lowered (with a corresponding rise in surface temperature). These cooler molecules insulate the surface from the higher temperature molecules further away from the surface, slowing convective heat transfer.

Figure 5. Convection-Laminar Flow

When velocity and/or turbulence increases, cooler molecules that have transferred energy to the surface are quickly replaced by higher temperature molecules, resulting in increased convective heat transfer as illustrated in Figure 6. This is the same phenomena as wind chill, except in this case, energy is transferred from a hot fluid (gas) to a solid surface rather than from a hot surface (i.e., your skin) to a cooler fluid (air).

Figure 6. Convection-Turbulent Flow

More to Follow

Subsequent posts in this series will examine radiant heat transfer and then move on into discussion of the process of combustion.

Ed Hartin, MS, EFO, MIFireE, CFO

References

Kerber, S. & Madrzykowski, D. (2009) Fire Fighting Tactics Under Wind Driven Fire Conditions: 7-Story Building Experiments, NIST Technical Note 1629. Gaithersburg, MD: National Institute of Standards and Technology.