Gas Cooling
Saturday, August 14th, 2010In a compartment fire, the upper layer presents a number of hazards to firefighters including the fact that 1) Smoke is fuel, and 2) the upper layer can be extremely hot. Application of an appropriate amount of water fog into the upper layer reduces the potential for ignition and lowers the temperature of the gases (reducing thermal load on the firefighters working below). While this sounds simple, and fairly intuitive, this basic technique to control upper layer hazards is frequently misunderstood. This is the first in a series of posts that will attempt to provide a simple explanation of the science behind gas cooling as a fire control technique.
How Does it Work
When a pulse (brief application) of water fog is applied into a layer of hot smoke and gases with a temperature of 500o C (932o F) what happens? As the small droplets of water pass through the hot gas layer, energy is transferred from the hot smoke and gases to the water. If done skillfully, the upper layer will not only be cooler and lest likely to ignite, but it will contract (or at least stay the same volume) providing a safer working environment below.
As demonstrated by Superintendent Rama Krisana Subramaniam, Bomba dan Penelamat (Fire & Rescue Malaysia) a short pulse can place a large number of small water droplets in the upper layer that develops during a compartment fire (see Figure 1).
Figure 1. Short Pulse
When presenting this concept, firefighters often present me with two questions:
- Since water expands approximately 1700 times when turned to steam at 100o C, why doesn’t the upper layer drop down on top of the firefighters?
- How can such a small amount of water have such a dramatic effect on the fire environment?
Math or No Math?
Using a bit of math, there is a really good explanation as to how gas cooling really works. The best answer is a bit complex, but a good conceptual explanation can be accomplished with a minimal amount of math.
Heating the water to 100o C (212o F) and production of steam transfers a tremendous amount of energy from the hot smoke and gases to the water, reducing the temperature of the hot gases. As the temperature of the hot gases is reduced so is their volume. However, don’t forget about the steam.
When water is turned to steam, it expands. At its boiling point, water vaporized into steam will expand 1700 times. A single liter of water will produce 1700 liters (1.7 m3) of steam. The expansion ratio when water is vaporized is significant. However, due to the tremendous amount of energy required to vaporize the water (and resulting reduction in gas temperature), the final volume of the mixture of hot gases and steam is less than the original volume of hot gases within the compartment.
The Key
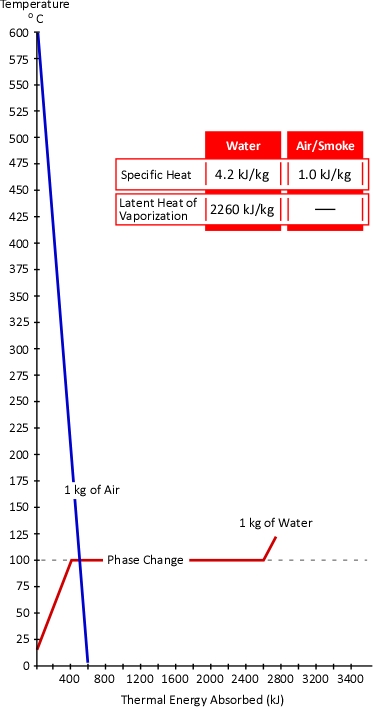
The temperature of the gases is lowered much more than the temperature of the water is increased. Why might this be the case? The key to this question lies in the concepts of specific heat and latent heat of vaporization. As illustrated in Figure 2, the specific heat of smoke is approximately 1.0 kJ/kg (Särdqvist, 2002; Yuen & Cheung, 1999) while the specific heat of water is 4.2 kJ/kg and even more importantly the latent heat of vaporization of water is 2260 kJ/kg. What this means is that it requires over four times the energy to raise the temperature of a kilogram of water by 1o C than it does to lower the temperature of smoke by the same amount. In addition, it requires 2260 times the energy to turn 1 kg of water to steam at 100o C than it does to lower the temperature of 1 kg of smoke by 1o C.
Figure 2. Heating and Cooling Curves of Smoke & Water
While water expand as it turns to steam, the hot gas layer will contract as it’s temperature drops. At the same pressure, change in the volume of a gas is directly proportional to the change in absolute temperature. If the initial temperature of the hot gas layer is 500o C (773 Kelvin) and its temperature is lowered to 100o C (373 Kelvin) the absolute temperature is reduced by slightly more than half (773 K-373 K=400 K). Correspondingly the volume of the hot gases will also be reduced by half.
An Example
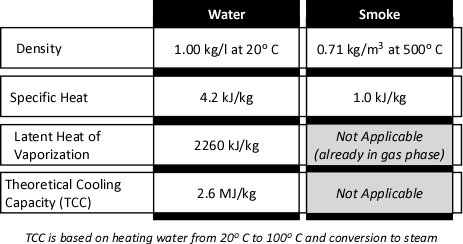
Once the underlying concept of gas cooling has been explained, the question of how a small amount of water can have such a dramatic effect may still remain. After all, the preceding explanation compared a kilogram of water to a kilogram of air. Firefighters normally do not usually think of either of these substances in terms of mass. Water is measured in liters or gallons. If measurement of smoke and air is thought of, it would likely be in cubic meters (m3) or cubic feet (ft3). Sticking with SI units, consider the properties of water and smoke as illustrated in Figure 3:
Figure 3. Properties of Water and Smoke
While over simplified, the compartment fire environment can be considered as being comprised of two zones; a hot upper layer and a cooler lower layer, each with reasonably uniform conditions (this is the approach used by computer models such as the Consolidated Model of Fire and Smoke Transport, CFAST).
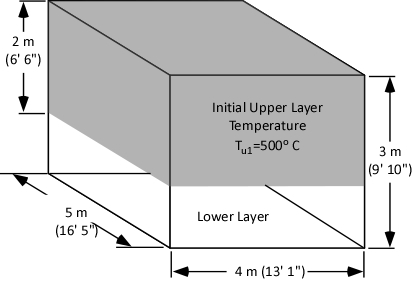
As illustrated in figure 4, our examination of gas cooling will consider a single compartment 4 meters (13’ 1”) wide and 5 meters (16’ 5”) long with a ceiling height of 3 meters (9’ 10”). The upper layer comprised of hot smoke and air is two meters deep and has an average temperature of 500o C (932o F).
Figure 4. Compartment with Two Thermal Zones
What volume of water must be applied into the upper layer to reduce its temperature from 500o C to 100o C?
Just as input of energy is required to increase temperature, energy must be transferred from a substance in order to lower its temperature. The first step in determining the water required for cooling is to calculate the energy that must be transferred from the upper layer to achieve the desired temperature reduction.
The specific heat of smoke is approximately 1.0 kJ/kg. This means that 1.0 kJ of energy must be transferred from a kilogram of smoke in order to reduce its temperature by 1o C. This requires that we determine the mass of the upper layer.
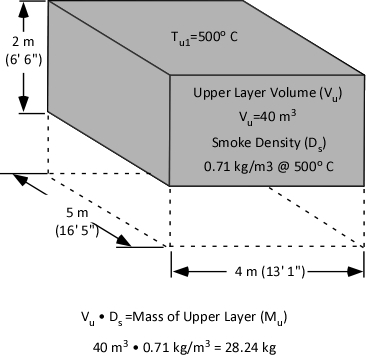
Calculation of mass involves multiplying the volume of the upper layer (40 m3) by the (physical) density of smoke (0.71 kg/m3) at the average temperature of the upper layer (500o C) as illustrated in Figure 5.
Figure 5. Mass of the Upper Layer
Specific heat is the energy required to raise the temperature of a given unit mass of a substance 1o. The same energy must be also be transferred to lower the temperature of a unit mass of a substance by 1o. As illustrated in Figure 3, the specific heat of smoke is 1.0 kJ/kg. Therefore, to lower the temperature of a single kilogram of smoke by 1o C, 1.0 kJ must be transferred from that kilogram of smoke. With an upper layer mass (Mu) of 28.24 kg, 28.24 kJ must be transferred from the upper layer to water applied for gas cooling in order to reduce its temperature by 1o C.
Reduction of upper layer temperature from 500o C to 100o C is a change of 400o. Multiplying 28.24 kJ by 400 determines the total amount of energy that must be transferred to water applied for gas cooling in order to reduce the temperature to 100o C. As illustrated in Figure 6, 11,296 kJ (11.3 MJ) must be transferred from the upper layer to the water to effect a 400o C reduction in temperature.
Figure 6. Energy Transfer Required
Now that we have determined the energy that must be transferred from the upper layer in order to lower the temperature from 500o C to 100o C, it is possible to identify how much water must be applied to accomplish this task. However, that will be the topic of my next post. In addition, I will provide an explanation as to why the volume of the upper layer does not (necessarily) increase when water applied to cool the gases turns to steam.
Ed Hartin, MS, EFO, MIFireE, CFO
References
Särdqvist, S. (2002). Water and other extinguishing agents. Karlstad, Sweden: Räddnings Verket.
Yuen, K. & Cheung, T. (1999). Calculation of smoke filling time in a fire room – a simplified approach. Journal of Building Surveying, 1(1), p. 33-37