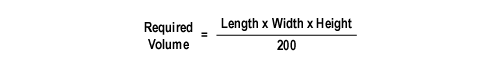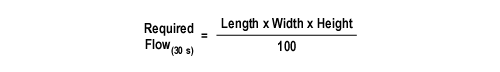Posts Tagged ‘fire flow’

As discussed in Estimating Required Fire Flow: The National Fire Academy Formula, there are a number of ways to estimate required (total) fire flow or tactical rate of flow (required for fire attack). This post examines the groundbreaking work of Keith Royer’s and Floyd W. (Bill) Nelson’s work in development of a method to identify the volume and flow of water necessary for fire control with water fog.

The fire service often accepts (or rejects) concepts, theories, and practices based on what is written in training manuals, trade magazines, or presented by well known speakers. Others take the message and pass it along, trying to improve or simplify the message. Much can be lost in the translation. While we are strongly influenced by tradition, we occasionally forget history, and valuable work that was done by our predecessors is forgotten or misinterpreted. This is particularly true in the case with regard to Royer’s and Nelson’s volume and rate of flow formulas.

Origins of the Iowa Formula

In 1951, Keith Royer and Floyd W. (Bill) Nelson were hired by Iowa State University to manage the Engineering Extension Service Firemanship Training Program. Royer and Nelson both became involved in the Exploratory Committee on the Application of Water, a research team comprised of fire service, fire protection engineering, and fire insurance representatives. The principal work of the Exploratory Committee was investigation of the use of water fog for firefighting.

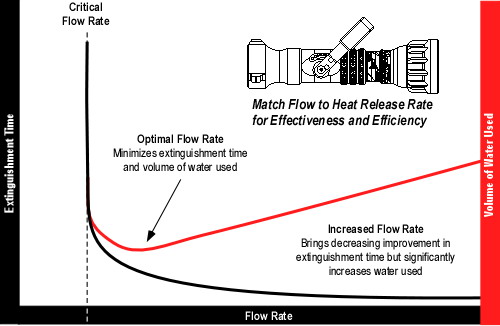
One critical question faced by Royer and Nelson was how much water was necessary to control a fire with water fog? In his book Qualitative Fire Behavior (1989), Nelson observed: “In principle, firefighting is very simple. All one needs to do is put the right amount of water in the right place and the fire is controlled.”� Royer and Nelson recognized that heat release from the fire must be balanced by the energy required to heat water to its boiling point and change it to steam. Through their research, they discovered that too little or too much water was considerably less effective than the right amount.

Note: While math is considerably simpler when using standard international (SI) units, Royer and Nelson did their work in traditional units (e.g., feet, gallons, British thermal units, degrees Fahrenheit). For now, I will stick with traditional units to illustrate how the Iowa Formula was developed. Safe and Effective Use of Fog Nozzles: Research and Practice (Wiseman & Bertrand, 2003) includes adaptation of the formula to the use of SI units.

Based on the results of their research on extinguishing compartment fires, Royer and Nelson developed the following formula to determine the volume of water (in gallons) required to control a fire in a given size compartment.

Royer and Nelson based this formula on the following two concepts:

1. Water converted to steam expands at a ratio of 1700:1, as a result one gallon of water (0.13 ft³) produces 221 ft³ of steam. However, in practical application it is unlikely that all of the water would be converted to steam. Royer and Nelson estimated the efficiency of this conversion at 90%, resulting in production of 198.9 ft³ of steam per gallon. They rounded this value to 200 to simplify calculation.
2. In 1955 the Factory Mutual Laboratories determined that oxidization of ordinary fuel with 1 ft³ of oxygen (at standard temperature and pressure) resulted in release of 535 British thermal units (Btu) of energy. Based on an atmospheric oxygen concentration of 21% and substantive reduction or cessation of flaming combustion at 15% concentration, Royer and Nelson estimated that seven percent (of atmospheric concentration of oxygen) was available to support flaming combustion. This led them to estimate that combustion of ordinary fuel with 1 ft³ of air would result in release of 37 Btu. Combustion of ordinary fuel with 200 ft³ of air (would therefore release 7,400 Btu. One gallon of water, raised from a temperature of 62^o F to 212^o F and completely converted to steam will absorb 9330 Btu. As with their calculation for steam production, an efficiency factor of 90% can be applied, resulting in absorption of 8397 Btu. This illustrates that a single gallon of water converted to steam will absorb the energy released by combustion of ordinary fuel with 200 ft³ of air.

Note: There are a few problems in using volume when discussing the energy released based on the quantity of oxygen or air in the combustion reaction. Chief of which is the variation in volume based on temperature. It would be more appropriate to speak to the mass of oxygen or air. However, Royer and Nelson based their approach on volume, so we will follow this line of reasoning (recognizing that while it is simple to understand, it has significant limitations).

Royer and Nelson used these concepts to support their formula to determine the volume of water required to control a fire with water fog.

Volume and Flow Rate

The volume formula, while a good start, still did not identify the required flow rate. The required volume could be delivered over various periods of time and still control the fire. If water was applied over a one minute period, the volume formula could be used to determine flow rate directly. However, Royer and Nelson estimated if water was applied in the right place, most fires could be controlled (but not necessarily extinguished) with water fog in less than 30 seconds. Given this timeframe, the volume formula translated into the rate of flow formula as follows:

Limitations

The Iowa Rate of Flow Formula is designed to estimate the flow rate required to control a fire in a single open area of a building with a 30 second application of water fog. This approach requires foreknowledge of the building and made the Iowa rate of flow formula most suited for preplanning, rather than tactical application.

That said, this does not mean that you cannot apply this formula (or its concepts) tactically based on the estimated area of involvement in a building that has limited compartmentation (e.g., multiple, interconnected compartments, open doors, unprotected shafts). However, it is essential to remember that Royer and Nelson based their formula on a 30 second application (potentially from multiple points) outside the compartment, and not working your way from compartment to compartment as is typically done in offensive, interior firefighting operations.

Additional Considerations

The concept that water applied to the fire compartment will turn to steam and fill the space, displacing air and hot smoke is a foundational principle of the indirect and combination attack as discussed by Lloyd Layman, Keith, Royer and Bill Nelson. This physical reaction is also commonly accepted as fact within the fire service. However, the science is a bit more complicated.

Royer and Nelson are correct in assuming that at its boiling point water converted to steam will expand 1700 times and not increase in temperature. However, water converted to steam while passing through the hot gas layer does not increase the total volume of gas and vapor in the space. The expansion of steam is more than counterbalanced by contraction of the hot gas layer due to cooling. On the other hand, water that passes through the hot gas layer (without taking energy from the gases) and converts to steam on contact with compartment linings (walls, ceiling) results in addition of the volume of steam to the volume of air and smoke in the compartment. This is not commonly understood and will be the subject of a later post. Steam formed at 212^o F (100^o C) can continue to absorb energy if the temperature of the fire environment is above 212^o F (100^o C) and will continue to expand (while the hot gases correspondingly contract).

One of the fundamental assumptions central to the Iowa formula is that the oxygen available to the fire is limited to that contained within the volume of the fire compartment. However, this is unlikely. If smoke is visible, ventilation (i.e., exchange of the atmosphere in the compartment with outside air) is taking place to some extent. In addition, if the compartment is not totally isolated from the remainder of the building, air track (movement of smoke and air) will provide additional oxygen to the fire. However, Royer and Nelson did identify an extremely important and often overlooked point. The Iowa tests showed that the heat release rate from actual compartment fires was less than the value based on the potential heat release from the fuel involved due to limitations in ventilation.

In a compartment fire, heat release rate is often (except in the incipient and early growth stage) limited by ventilation. One of the most important lessons that can be learned from Royer’s and Nelson’s work is that the flow rate and volume of water required for fire control is related not only to the method of attack, but also to the ventilation profile of the compartment or building involved.

Building on the Past

The National Fire Academy Fire Flow Formula (see Estimating Required Fire Flow: The National Fire Academy Formula) is based on synthesis of the experience of a group of experienced fire officers. On the other hand, the Iowa Formula is based on analysis of extensive empirical evidence developed during live fire tests. These formula each have different assumptions and are designed for different purposes. However, both provide useful information if they are used as intended. Future posts will examine the topic of fire flow from an international perspective, looking at the approaches taken by Cliff Barnett from New Zealand and my colleague Paul Grimwood from the United Kingdom.

For more information on Fire Flow, visit Paul Grimwood’s website www.fire-flows.com. Paul has amassed a tremendous amount of information on this topic from around the world.

Ed Hartin, MS, EFO, MIFireE, CFO

Application of the appropriate flow rate is critical to fire control. However, how can we estimate the flow rate that is necessary?

There are a number of methods that can be used to estimate or calculate required flow rate for fire control. One method is to simply use your experience (which may work quite well if you have been to a large number of fires and paid attention to flow rate). However, if you do not have a large base of experience to draw on or need to apply flow rate estimation in a preplanning context, other methods are necessary. One of the most common methods used in the United States is the National Fire Academy (NFA) Fire Flow Formula.

Development of the NFA Formula

In the mid 1980s the development team for the National Fire Academy Field course Preparing for Incident Command developed this formula to provide a simple method for estimating the flow requirements for offensive, interior operations where a direct attack was used to control and extinguish the fire.

Interestingly enough the NFA Fire Flow Formula is not based on science (at least not physical science). The developers tapped into another valid source of information, knowledge of experienced fire officers.

The course developers designed a number of plot and floor plans showing different sizes of building with different configurations (e.g., rooms, doors, windows) with varied levels of involvement. These drawings were distributed to students attending the academy and they were asked how their fire department would control the fire (with the emphasis on the number, placement, and flow rate of hoselines).

There are three major parameters used for the scenarios based on these plot and floor plans.

• All scenarios were designed to involve offensive, interior firefighting operations and as such, fire involvement was limited to 50% or less of the total floor area of the building.
• Operations were to be conducted as they normally would, with initial operations started by the first arriving company and additional tactics implemented as resources arrive.
• Primary search and ventilation tactics would be performed concurrently with fire control operations.

The student’s responses were collected and analyzed. For each scenario, when the floor area of the involved area in square feet (ft²) was divided by the total flow rate in gallons per minute (gpm) for all hoselines used for attack, backup, and exposure protection; the average result was three. Turning this around, flow rate in gpm can be determined by dividing the area of involvement in ft² by three.

In that the exterior of the building can be determined more easily than the area of involvement, the formula was adapted to determine the flow rate based on building size and approximate percentage of involvement as illustrated below:

Note: This method does not translate easily into standard international (SI), simply converted the formula would be lpm = M²/0.07.

The course development team extended the application of this formula to include estimated flow required for exposure protection by adding 25% of the flow rate required for fire control (as determined by the basic formula) for each exposure. The full formula as used in preplan development is as follows:

The development team believed that this formula would also be applicable to defensive attack for levels of involvement above 50%. However, this was not validated using the same type of methodology as used to develop the base fire flow formula.

Limitations

It is important to remember the limitations of this fire flow estimation method:

• The NFA Fire Flow Formula is designed for offensive, interior operations involving direct attack.
• The formula becomes increasingly inaccurate if the level of involvement exceeds 50% or the resulting flow is greater than 1,000 gpm.
• This method is not designed for defensive, master stream operations (even though the developers believed that it would provide a reasonable estimate of required flow rate for defense.
• The formula is based on area, not volume. If the ceiling height exceeds 10’, the flow rate may be underestimated.
• The NFA Formula does not take into account the potential heat release rate of the fuel. Fuel with extremely high heat release rate may require a higher flow rate
• The developers of the NFA Formula made the assumption that the building was well ventilated (tactically). Increased ventilation can (if the fire is initially ventilation controlled) result in increased heat release rate.
• It may be tough to do the math at 0200 hours when faced with a rapidly developing fire! This method is best used in advance of the fire when developing preplans or working on tactical problems

Total Versus Tactical Rate of Flow

The most common application error is the belief that the formula determines the flow rate required for fire attack. This is incorrect! The formula determines the total flow rate required for attack, backup, and exposure protection lines. Use of this formula to determine the flow rate for the initial attack line (or lines) will greatly overestimate the required tactical rate of flow.

As discussed in It’s the GPM! and Choose your Weapon Part I, substantially exceeding the required tactical rate of flow has diminishing returns on speed of extinguishment and substantially increases the amount of water used. If excessive, water that is not used efficiently (i.e., turned to steam) increases fire control damage).

Using the NFA Base Fire Flow Formula (no exposures), roughly half of the flow rate is used for attack lines and the remainder is used for backup lines. The NFA formula provides an excellent method for estimating total flow rate requirements (which impacts on water supply and resource requirements). However, it must be adjusted (reduced by half) to determine the tactical rate of flow necessary for direct attack on the fire.

Other Approaches

As outlined in this post, the NFA Fire Flow Formula is intended for estimating the total flow rate required when making a direct attack and has a number of specific parameters that must be considered. Prior to introduction of the NFA formula, the Iowa Fire Flow Formula developed by Floyd W. (Bill) Nelson and Keith Royer. The Iowa Formula was developed quite differently, has substantially different assumptions, and will be the subject of my next post.

For more information on Fire Flow, visit my colleague Paul Grimwood’s website www.fire-flows.com. Paul has amassed a tremendous amount of information on this topic from around the world.

Ed Hartin, MS, EFO, MIFireE, CFO

I recently read an article in the October issue ofFire Engineering magazine titled Improving Preconnect Function and Operation. The author, LT Bob Shovald, described how his department approached the process of improving operations with small, preconnected handlines and focused on three critical factors in effective engine company operations: 1) Hose diameter and flow rate, 2) nozzle selection, and 3) hoseloads. LT Shovald made a number of good points, but misconnected on the basic science behind effective and efficient use of water for fire control.

Flow Rate

LT Shovald makes a case for high flow handlines based on changes in the built environment that influence potential fire behavior.

Primarily it comes down to one important factor, gallons per minute (gpm). Using 95- and 125-gpm attack lines is outdated and dangerous.

• Because of the huge increase of synthetic materials in modern homes and businesses, including foams, plastics, vinyl, and volatile coatings, we are now experiencing fires with higher rates of release than ever before.
• Because of the high cost of energy, more homes and businesses have improved insulation. In a fire, this seals that increased heat inside the structure.
• As a result of more effective fire prevention programs, we arrive on-scene much sooner than in years past, in large part thanks to inexpensive smoke detectors.

What this adds up to is that we are getting on-scene sooner to hotter, more aggressive fires, often just before flashover conditions or self-ventilation. To fight the beast, today we need a bigger gun with bigger bullets (i.e., proving the greater gpm and thus more water faster at the start of our interior attacks). The gpm not the pressure and not the steam kill the beast.

LT Shovald’s argument for high flow handlines sounds reasonable. However, there are a few problems once you look past the surface.

Fire Power vs. Firefighting Power

LT Shovald correctly makes the connection between heat release rate and flow rate necessary for fire control. All too often, firefighters think that it takes “gpm to overcome Btu”�. However, British thermal units (Btu) like Joules (J), are a measure of energy, not its release rate. Heat release rate is expressed in units of energy per unit of time, such as Btu/minute or watts (J/s).

Heat release rate is the most critical factor compartment fire development. If heat release rate is insufficient (e.g., a small fire in a metal trash can) the fire will not flashover or reach the fully developed stage. On the other hand, if the fire involves a recliner or couch, heat release rate is likely to be sufficient for the fire to grow and rapidly transition through flashover to the fully developed stage.

However, there is another critical factor in this scenario. Oxygen is required for the fire to release the chemical potential energy in the fuel. If doors are closed and windows are intact, the fire may quickly consume much of the available oxygen. If this occurs, heat release rate is limited by ventilation and fire growth slows.

LT Shovald states that “it’s the gpm,� not the pressure, and not the steam” that extinguishes the fire. Flow rate is critical, but this is not entirely correct. Water is an excellent extinguishing agent because it has a high specific heat (energy required to raise its temperature) and high latent heat of vaporization (energy required to change it from water to steam). Of these two factors, conversion of water to steam is most significant as it absorbs 7.5 times more energy than heating water from 20^o C ( 68^o F) to its boiling point. The firefighters power is not simply related to flow rate, but flow rate effectively applied to transfer heat from hot gases and surfaces by changing its phase from liquid (water) to gas (steam). Extinguishing a compartment fire generally involves converting a sufficient flow (gpm or lpm) of water to steam. So while the “steam”� itself does not generally extinguish the fire, the energy absorbed in turning the water to steam has the greatest impact on fire extinguishment.

Changes in the Built Environment

LT Shovald is correct that many of the synthetic fuels used in today’s buildings have a higher heat of combustion (potential chemical energy) and given sufficient ventilation have a higher heat release rate when compared to materials such as wood and paper. True to their design, modern, energy efficient buildings retain energy during fire development, speeding the process. However, this type of building also controls normal ventilation (the building is not as “leaky” as older structures) and energy efficient windows are far less likely to fail and change the ventilation profile. As a consequence, the fire department is likely to encounter ventilation controlled fires where heat release rate is limited by the available oxygen. Early detection may also influence fire conditions as firefighters may arrive to find a pre-flashover growth stage fire when heat release has not yet peaked.

The key here is that flow rate must be sufficient to meet or exceed the fires heat release rate. Arriving earlier in the fires growth and building characteristics leading to a ventilation controlled fire, do not necessarily lead to the need for a higher flow rate, on the contrary, the required flow rate during the growth stage is actually lower than that for a fully developed fire (when heat release rate is at its maximum). However, firefighters must also consider potential increase in heat release rate that result from tactical ventilation or unplanned changes in the ventilation profile (e.g., failure of a window).

One excellent point in supporting the argument for high flow handlines that LT Shovald did not raise is the large volume (floor area and ceiling height) and limited compartmentation encountered in many contemporary homes. Older homes generally had smaller rooms and were more highly compartmented. Many new homes have spacious and open floor plans, in some cases with multi-level atriums and high ceilings. In addition to frequently having open floor plans, many of these buildings are also have an extremely large floor area. This type of structure presents a significantly different fire problem and often requires a much higher flow rate than a more traditional, highly compartmented residence.

Tactical Flow Rate

While I agree with LT Shovald regarding the value of high flow handlines, his statement that 95 and 125 gpm are “outdated and dangerous” is unsupported. Safe, effective and efficient fire control requires:

• Water application to control the fire environment as well as direct attack on the fire
• Appropriate flow rate for the tactical application (cooling hot, but unignited gases may be accomplished at a lower flow rate than direct attack on the fire)
• Direct attack to exceed the critical flow rate based on the fires heat release rate
• Sufficient reserve (flow rate) be available to control potential increases in heat release rate that may result from changes in ventilation
• Water application in a form appropriate to cool its intended target (i.e., small droplets to cool hot gases or to cover hot surfaces with a thin film of water).
• Water to reach its intended target (fog stream to place water into the hot gas layer and a straight or solid stream to pass through hot gases and flames and reach hot surfaces)
• Control of the fire without excessive use of water

A flow rate of 95 or 125 gpm is only dangerous if firefighters attempt to use it to control a fire which requires (or has the potential to require) a higher flow rate. While a high flow rate will quickly extinguish a small fire, this generally results in use of considerably more water as illustrated below.

Effective and efficient fire control requires that we match the flow rate to the task at hand. At the simplest level this means using 1 �”� (38 mm) or 1 �”� (45 mm) handlines for smaller fires and 2″� (50 mm) or 2 �”� (64 mm) handlines for larger fires. It may also mean placing control of flow rate in the nozzle operators hands by using a variable flow or automatic nozzle and letting the firefighter select the flow rate based on the tactical situation.

Ed Hartin, MS, EFO, MIFireE, CFO